img

Junpeng

Welcom from Junpeng

Junpeng Wan /dʒuːn.pɛŋ wɑːn/ (joon-peng wahn) 万俊鹏

Blog

Computer Security & Systems

ARM BTB reverse engineering

| Read: times | Author: Junpeng Wan

catalog

Intro

One year and a half ago, I needed to figure out the BTB(branch target buffer) capacity of an ARM server. However, no public documents could be found then. The good news was that previous work reverse engineered BTB capacity on x86 architectures[1][2]. And I am luckily enough to reproduce it and according to my results on Kunpeng 920, the BTB capacity is 4K. My code can be found here.

Details

My method is to count an PMU event called ARM_PMU_BR_MIS_PRED when executing a bunch of branches. This event will tell us if there is a mispredicted or not predicted branch[3].

The following pseudocode is our test gadget, which consists of fall-through unconditional indirect branches. We control the branch number B and the align distance N, where N is the gap(bytes) between two labels(or basic blocks).

adr x0, next1
BR X0
nop
nop
.......(some other nops)
nop
 
next1:
adr x0, next2
BR X0
nop
nop
.......(some other nops)
nop
 
next2:
adr x0, next3
BR X0
nop
nop
.......(some other nops)
nop
 
next3:
ret

We count branch misprediction rates for different B and N. For each test, we first execute our test gadget 10 times to warm up the BTB; secondly, we run the test gadget once and log the difference of the PMU event counter(C). Then the branch misprediction rate is C/B. The result is in the following diagram.

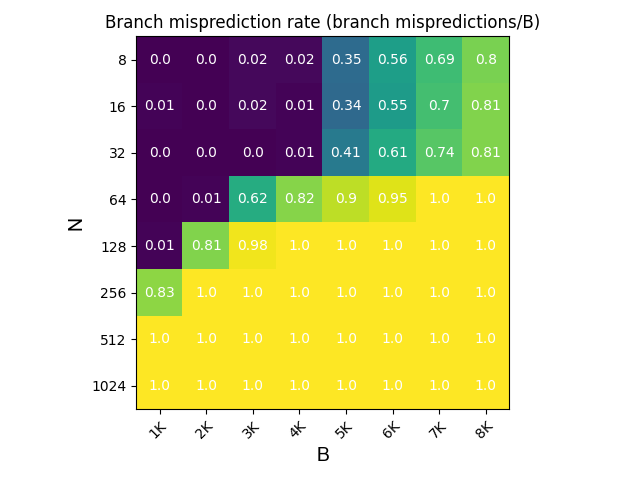
From the diagram, we could know:

  • BTB set index starts from bit 5. Because if B goes from 3K to 7k, the misprediction rate is almost the same if N goes from 16 to 32(32=2^5); but there is a leap from 32 to 64.
  • The BTB entry size is 4096. Because when N is 32, the rate is 0.01 for 4K however 0.39 for 5K. However, there are still 40-50 branches not buffered by BTB. It may be introduced by timer interrupts or other noise.

A little bit more

I am not sure with the following contents and welcome to correct me.

Ways

We already knew that the set index starts from bit 5. Since the BTB capacity is 4K, the set index bits are at most 12 bits (2^12=4096). Therefore, if we let N >= 2^17, all branches will fit into the same set. By counting branch mispredictions, we could know the ways in each set. Here is our result. 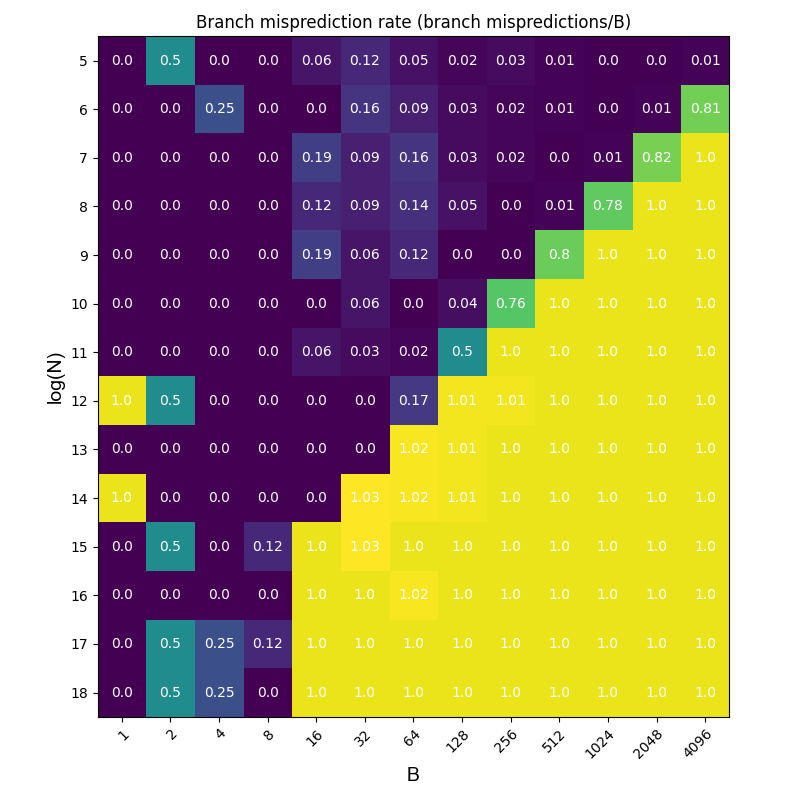From the picture, we may conclude that each set has 8 ways. Because when B=8, there is always a low miss rate when log(N)>17. However, if there a eviction buffer for BTB, the ways maybe smaller(like 4 or 6). If way=8, then there are 512 sets(8512=4096). The set index should be 5-13 bit. However, we observe that when log(N) = 14 and B=16, the cache miss rate is 0, which implies that the 16 branches are held by different sets so bit 14 is also used for indexing sets. As the picture shows, each bit from 5 to 14 could influence the set distribution thus influencing results. There should be a hash function which maps 5-13 bit to 512 BTB sets. If way=4, and there exists a BTB eviction buffer, then there are 1024 sets(41024=4096). The set index should be 5-14 bit.

According to Ockham’s razor principle, I tend to believe the BTB is 4 way and some eviction buffer exists. But more explorations need to be done to confirm that.

Reference